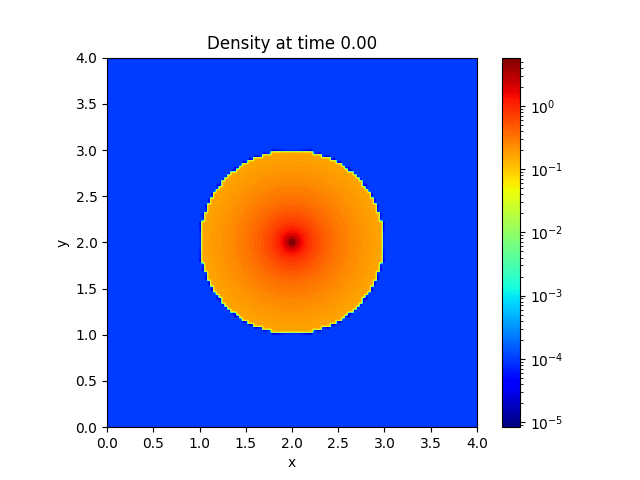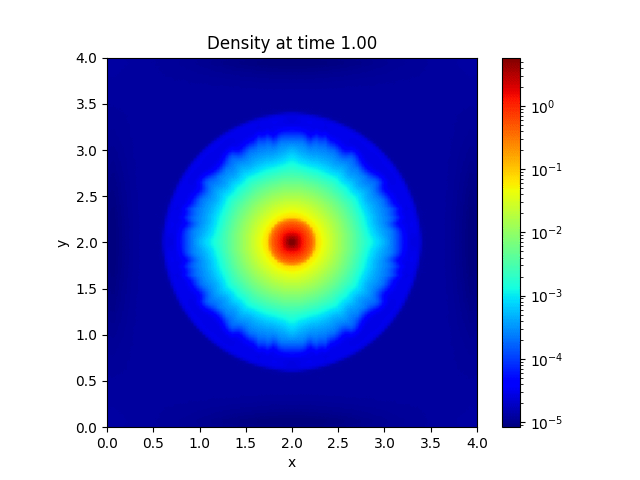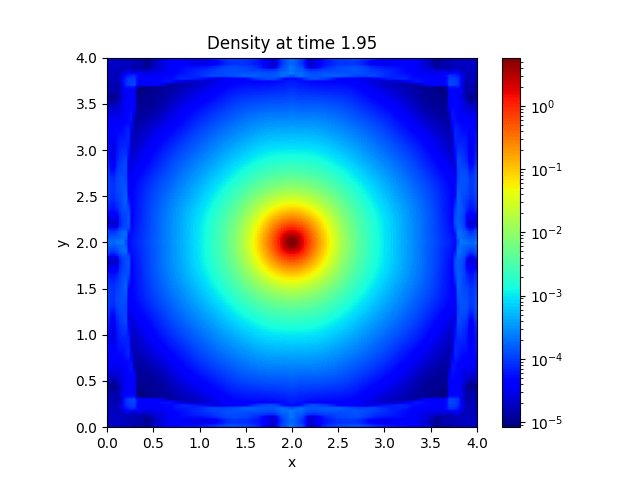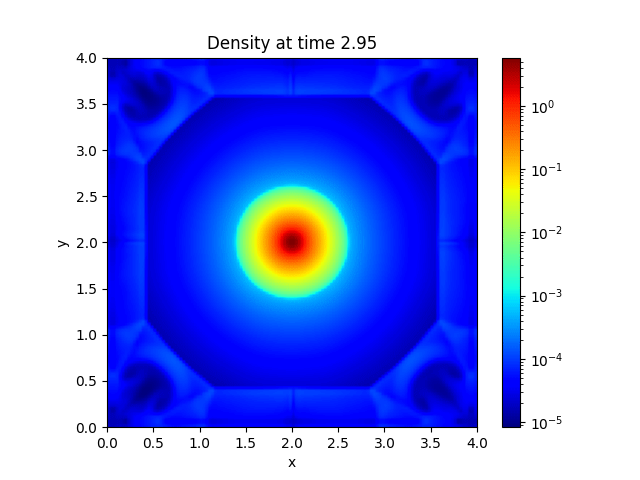
Introduction and Installation

jf1uids differentiable (magneto)hydrodynamics (MHD) for astrophysics written in JAX.

Fast and Differentiable

Written in JAX, jf1uids is fully differentiable - a simulation can be differentiated with respect to any input parameter - and just-in-time compiled for fast execution on CPU, GPU, or TPU.

Learn more »

Well-considered Numerical Methods

Divergence-free MHD based on Pang and Wu (2024) and conservative radial simulations based on Crittenden and Balachandar (2018).

Learn more »

Extensible

Physical modules, like one for stellar winds, can be easily added to the simulation. These modules can include parameters (or neural network terms) which can be optimized directly in the solver. Further primitive variables, like those for a cosmic ray fluid, are already implemented or can be added.

Learn more »

See also

The corresponding paper for the previous 1d-only version of this project is available on arXiv.

Installation

jf1uids can be installed via pip

pip install jf1uids

Note that if JAX is not yet installed, only the CPU version of JAX will be installed as a dependency. For a GPU-compatible installation of JAX, please refer to the JAX installation guide.

Tip

Get started with this simple example.

Showcase

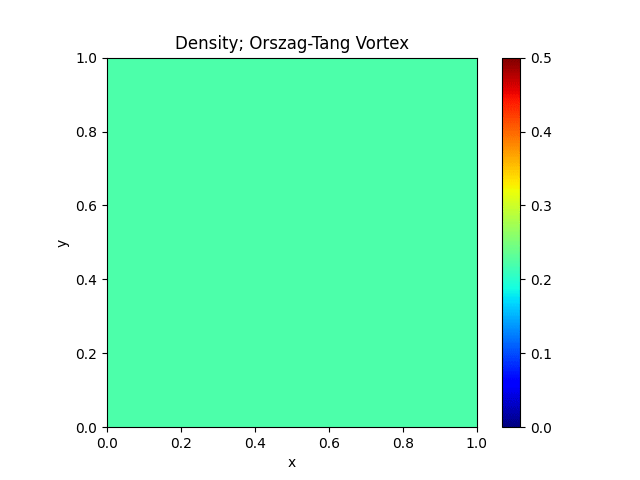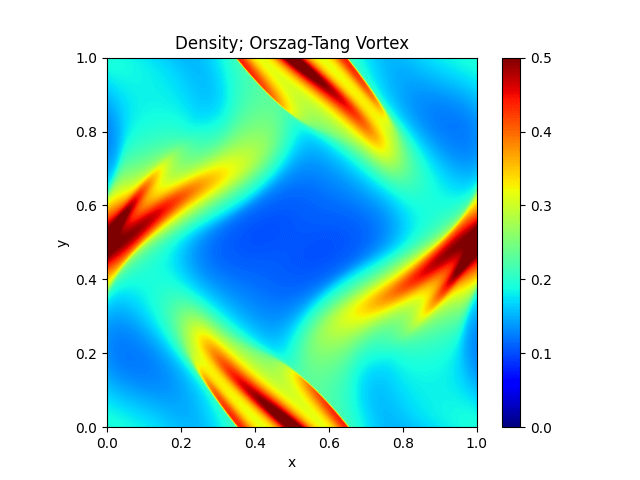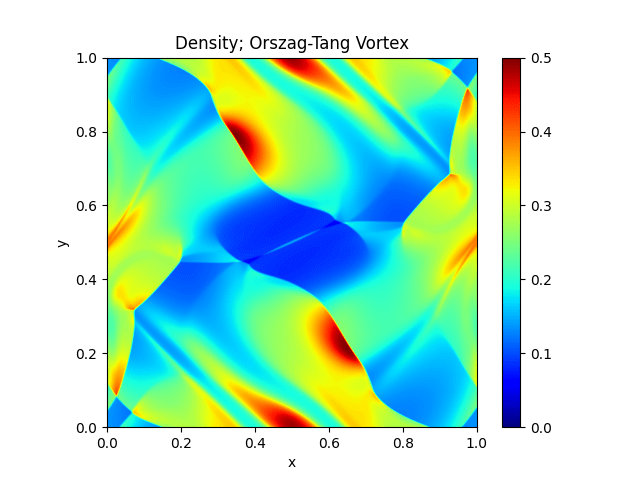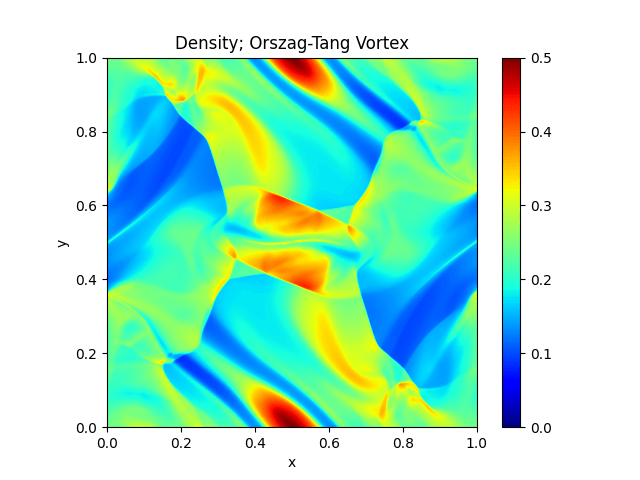
Orszag-Tang Vortex	3D Collapse

Gradients Through Stellar Wind

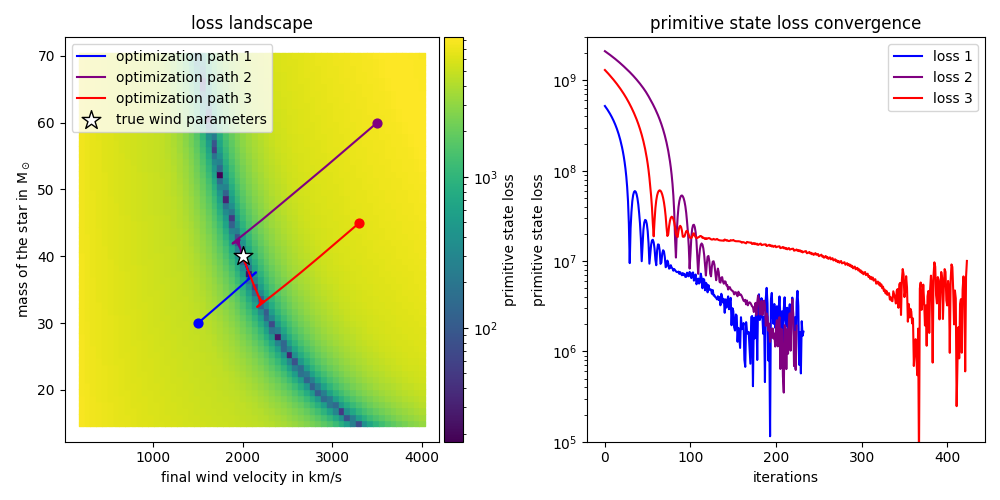
Wind Parameter Optimization

Notebooks for Getting Started

hydrodynamics

• Simple Example of a Simulation in jf1uids
• Conservational Properties
• 2D Kelvin Helmholtz Instability

magnetohydrodynamics

• Orszag-Tang Vortex

self-gravity

• Evrards Collapse

stellar wind

• Gradient Visualization for Radial 1D Stellar Wind Simulation
• Gradient Descent for Finding Stellar Wind Parameters
• Gradient Visualization for 3D Stellar Wind Simulation

Roadmap

See also

A baseline hydrodynamical code for dynamic adaptive mesh refinement (AMR) in JAX in one dimension, jamr, is available on GitHub.

• Implement a conservative 1d radial fluid solver with simple to implement yet powerful numerical schemes.

• Implement a simple stellar wind model, first analyses on the gradients of the final fluid state with respect to the wind parameters.

• Implementation of higher-order reconstruction methods like WENO-Z+, etc.

• Implementation of different Riemann solvers (currently HLL, HLLC, HLLC-LM)

• (advection-only) two-fluid cosmic-ray model

• cosmic ray diffusion

• Implementation of a shock finder

• Generalize to 2D and 3D

• implement self-gravity

• improve self-gravity for energy conservation