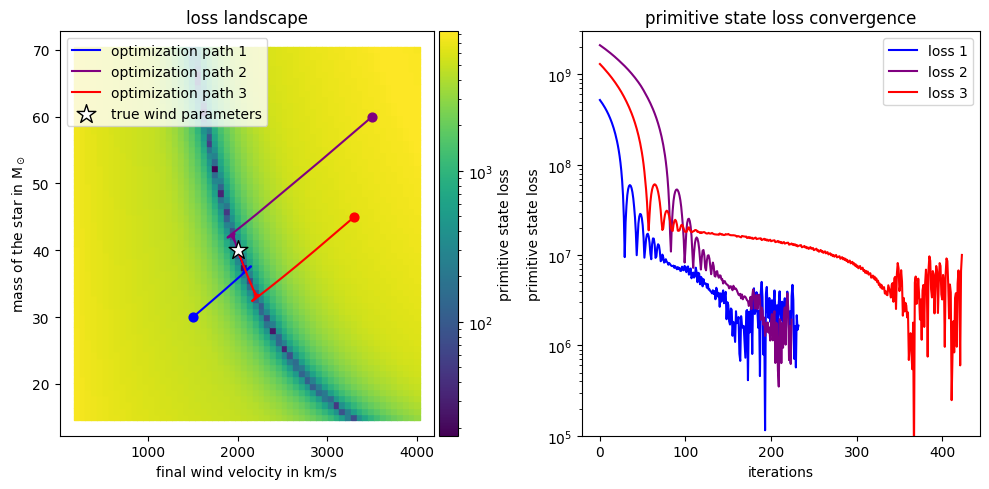
Gradient Descent for Finding Stellar Wind Parameters

Imports

# numerics
import jax
import jax.numpy as jnp
import optax

# plotting
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from mpl_toolkits.axes_grid1 import make_axes_locatable

# fluids
from jf1uids._physics_modules._stellar_wind.stellar_wind_options import WindParams
from jf1uids import strongest_shock_radius
from jf1uids import SimulationConfig
from jf1uids import get_helper_data
from jf1uids import SimulationParams
from jf1uids import time_integration
from jf1uids import get_registered_variables
from jf1uids.fluid_equations.fluid import construct_primitive_state


# units
from jf1uids import CodeUnits
from astropy import units as u
import astropy.constants as c

Initiating the stellar wind simulation

from jf1uids.option_classes.simulation_config import BACKWARDS, SPHERICAL
from jf1uids._physics_modules._stellar_wind.stellar_wind_options import WindConfig


print("👷 Setting up simulation...")

# simulation settings
gamma = 5/3

# spatial domain
geometry = SPHERICAL
box_size = 1.0

# ATTENTION: For testing we can take a lower resolution, the 3600 simulation
# for the loss-map from the paper with the settings from the paper take
# roughly 37 minutes and the gradient descents ~1h to run on the CPU
# of an AMD EPYC 7452 32-Core Processor.

fast_instead_paper = False

if fast_instead_paper:
    # Lower resolution is faster
    # especially as then we can also
    # take larger timesteps

    # setting for quick testing
    num_cells = 101
    # num_timesteps = 4000
else:
    # setting from the paper
    num_cells = 401
    # num_timesteps = 20000

fixed_timestep = False

differentiation_mode = BACKWARDS
num_checkpoints = 1000


# activate stellar wind
stellar_wind = True

# setup simulation config
config = SimulationConfig(
    geometry = geometry,
    box_size = box_size, 
    num_cells = num_cells,
    fixed_timestep = fixed_timestep,
    differentiation_mode = differentiation_mode,
    num_checkpoints = num_checkpoints,
    # num_timesteps = num_timesteps,
    wind_config = WindConfig(
        stellar_wind = stellar_wind,
        num_injection_cells = 10,
    ),
)

helper_data = get_helper_data(config)
registered_variables = get_registered_variables(config)

👷 Setting up simulation...

Setting the simulation parameters and initial state

# code units

from jf1uids.option_classes.simulation_config import finalize_config


code_length = 3 * u.parsec
code_mass = 1e-4 * u.M_sun
code_velocity = 1 * u.km / u.s
code_units = CodeUnits(code_length, code_mass, code_velocity)

# time domain
C_CFL = 0.8
t_final = 2.5 * 1e4 * u.yr
t_end = t_final.to(code_units.code_time).value
dt_max = 0.1 * t_end # not so important if the timestep criterion is good

params = SimulationParams(
    C_cfl = C_CFL,
    dt_max = dt_max,
    gamma = gamma,
    t_end = t_end
)

# homogeneous initial state
rho_0 = 2 * c.m_p / u.cm**3
p_0 = 3e4 * u.K / u.cm**3 * c.k_B

rho_init = jnp.ones(num_cells) * rho_0.to(code_units.code_density).value
u_init = jnp.zeros(num_cells)
p_init = jnp.ones(num_cells) * p_0.to(code_units.code_pressure).value

# get initial state
initial_state = construct_primitive_state(
    config = config,
    registered_variables = registered_variables,
    density = rho_init,
    velocity_x = u_init,
    gas_pressure = p_init,
)

config = finalize_config(config, initial_state.shape)

For spherical geometry, only HLL is currently supported.
Automatically setting reflective left and open right boundary for spherical geometry.
For stellar wind simulations, we need source term aware timesteps, turning on.

Setting up a reference simulation

sample_simulation = lambda velocity, mass_loss_rate: time_integration(initial_state, config, SimulationParams(
    C_cfl=params.C_cfl,
    dt_max=params.dt_max,
    gamma=params.gamma,
    t_end=params.t_end,
    wind_params=WindParams(
        wind_mass_loss_rate=mass_loss_rate,
        wind_final_velocity=velocity
    )
), helper_data, registered_variables)

# generate a reference simulation
M_star = 40 * u.M_sun
wind_final_velocity = 2000 * u.km / u.s
wind_mass_loss_rate = 2.965e-3 / (1e6 * u.yr) * M_star

reference_params = WindParams(
    wind_mass_loss_rate = wind_mass_loss_rate.to(code_units.code_mass / code_units.code_time).value,
    wind_final_velocity = wind_final_velocity.to(code_units.code_velocity).value
)

reference_simulation = sample_simulation(
    reference_params.wind_final_velocity,
    reference_params.wind_mass_loss_rate
)

reference_shock_radius = strongest_shock_radius(reference_simulation, helper_data, 10, 5)

Losses

def density_loss(vel_mass_loss):
    velocity = vel_mass_loss[0]
    mass_loss_rate = vel_mass_loss[1]
    final_state = sample_simulation(velocity, mass_loss_rate)
    return jnp.mean(jnp.abs(final_state[0] - reference_simulation[0]))

def full_profile_loss(vel_mass_loss):
    velocity = vel_mass_loss[0]
    mass_loss_rate = vel_mass_loss[1]
    final_state = sample_simulation(velocity, mass_loss_rate)
    return jnp.sum(jnp.abs(final_state - reference_simulation))

Loss map

def get_loss_map(velocity_range, mass_loss_rate_range):
    loss_map = jnp.zeros((len(velocity_range) * len(mass_loss_rate_range),))
    vel_list = jnp.zeros((len(velocity_range) * len(mass_loss_rate_range),))
    mass_list = jnp.zeros((len(velocity_range) * len(mass_loss_rate_range),))
    ind = 0

    for i, velocity in enumerate(velocity_range):
        for j, mass_loss_rate in enumerate(mass_loss_rate_range):
            loss_map = loss_map.at[ind].set(density_loss((velocity, mass_loss_rate)))
            vel_list = vel_list.at[ind].set(velocity)
            mass_list = mass_list.at[ind].set(mass_loss_rate)
            ind += 1
            print(f"Done {ind}/{len(velocity_range) * len(mass_loss_rate_range)}")
    return loss_map, vel_list, mass_list

# generate a loss map
mass_loss_rates = jnp.linspace(
    (2.965e-3 / (1e6 * u.yr) * 15 * u.M_sun).to(code_units.code_mass / code_units.code_time).value,
    (2.965e-3 / (1e6 * u.yr) * 70 * u.M_sun).to(code_units.code_mass / code_units.code_time).value,
    60
)

velocities = jnp.linspace(
    (200 * u.km / u.s).to(code_units.code_velocity).value,
    (4000 * u.km / u.s).to(code_units.code_velocity).value,
    60
)

loss_map, vel_list, mass_list = get_loss_map(velocities, mass_loss_rates)

Optimization

# We pick gradient descent for pedagogical and visualization reasons.
# In practice one would use e.g. Levenberg-Marquardt from the
# optimistix package.

def gradient_descent_optimization(func, x_init, learning_rate=20, tol=0.5, max_iter=2000):
    xlist = []
    x = x_init
    loss_list = []
    xlist.append(x)

    optimizer = optax.adam(learning_rate=learning_rate)
    optimizer_state = optimizer.init(x)

    for _ in range(max_iter):
        # Compute the function value and its gradient
        loss, f_grad = jax.value_and_grad(func)(x)
        loss_list.append(loss)
        
        # Update the parameter
        updates, optimizer_state = optimizer.update(f_grad, optimizer_state)
        x = optax.apply_updates(x, updates)
        xlist.append(x)
        
        # Check convergence
        if jnp.linalg.norm(updates) < tol:
            break
    
    return x, xlist, loss_list

Example loss paths

initial_guess1 = jnp.array([(1500 * u.km / u.s).to(code_units.code_velocity).value, (2.965e-3 / (1e6 * u.yr) * 30 * u.M_sun).to(code_units.code_mass / code_units.code_time).value])
x1, xlist1, loss_list1 = gradient_descent_optimization(full_profile_loss, initial_guess1)

initial_guess2 = jnp.array([(3500 * u.km / u.s).to(code_units.code_velocity).value, (2.965e-3 / (1e6 * u.yr) * 60 * u.M_sun).to(code_units.code_mass / code_units.code_time).value])
x2, xlist2, loss_list2 = gradient_descent_optimization(full_profile_loss, initial_guess2)

initial_guess3 = jnp.array([(3300 * u.km / u.s).to(code_units.code_velocity).value, (2.965e-3 / (1e6 * u.yr) * 45 * u.M_sun).to(code_units.code_mass / code_units.code_time).value])
x3, xlist3, loss_list3 = gradient_descent_optimization(full_profile_loss, initial_guess3)

Loss map plot

fig, axs = plt.subplots(1, 2, figsize=(10, 5))

divider = make_axes_locatable(axs[0])
cax = divider.append_axes('right', size='5%', pad=0.05)
norm = LogNorm(vmin=loss_map.min(), vmax=loss_map.max())
mapper = plt.cm.ScalarMappable(norm=norm, cmap=plt.cm.viridis)
plt.colorbar(mapper, cax=cax, orientation='vertical', label='primitive state loss')

axs[0].scatter((vel_list * code_units.code_velocity).to(u.km / u.s).value, (mass_list * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value, c=loss_map, cmap='viridis', norm=norm, s = 15, marker = "s")

axs[0].set_xlabel('final wind velocity in km/s')
axs[0].set_ylabel(r'mass of the star in M$_\odot$')
axs[0].set_title('loss landscape')

# plot the loss function
axs[1].plot(loss_list1, label='loss 1', color='blue')

# plot the optimization path
xlist1 = jnp.array(xlist1)
axs[0].plot((xlist1[:, 0] * code_units.code_velocity).to(u.km / u.s).value, (xlist1[:, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value, color='blue', label='optimization path 1')
axs[0].scatter(
    [(xlist1[0, 0] * code_units.code_velocity).to(u.km / u.s).value], [(xlist1[0, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value],
    c='blue', s = 40
)

# plot the optimization path
xlist2 = jnp.array(xlist2)
axs[0].plot((xlist2[:, 0] * code_units.code_velocity).to(u.km / u.s).value, (xlist2[:, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value, color='purple', label='optimization path 2')

axs[0].scatter(
    [(xlist2[0, 0] * code_units.code_velocity).to(u.km / u.s).value], [(xlist2[0, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value],
    c='purple', s = 40
)

# plot the loss function
axs[1].plot(loss_list2, label='loss 2', color='purple')

# plot the optimization path
xlist3 = jnp.array(xlist3)
axs[0].plot((xlist3[:, 0] * code_units.code_velocity).to(u.km / u.s).value, (xlist3[:, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value, color='red', label='optimization path 3')

axs[0].scatter(
    [(xlist3[0, 0] * code_units.code_velocity).to(u.km / u.s).value], [(xlist3[0, 1] * code_units.code_mass / code_units.code_time).to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value],
    c='red', s = 40
)

# plot the loss function
axs[1].plot(loss_list3, label='loss 3', color='red')

axs[1].set_xlabel('iterations')
axs[1].set_ylabel('primitive state loss')
axs[1].set_title('primitive state loss convergence')
axs[1].set_yscale('log')
axs[1].legend(loc='upper right')
plt.tight_layout()

# mark the true value as a red dot
axs[0].scatter(
    [wind_final_velocity.to(u.km / u.s).value],
    [wind_mass_loss_rate.to(2.965e-3 / (1e6 * u.yr) * u.M_sun).value],
    c='white', s = 200, label='true wind parameters', marker = "*", zorder = 10, edgecolors='black'
)

axs[0].legend()
axs[1].legend()

# axs 1 y lim 10^6 to 3 * 10^9
if fast_instead_paper:
    axs[1].set_ylim(1e5, 3e9)
else:
    axs[1].set_ylim(1e6, 3e9)

plt.savefig('../figures/wind_parameter_optimization.png')